学习笔记 Evidential Deep Learning(EDL)证据深度学习
本文最后更新于:2024年2月25日 下午
学习笔记 Evidential Deep Learning(EDL)证据深度学习
证据深度学习是文献Evidential Deep Learning to Quantify Classification Uncertainty中提出的一种衡量模型预测不确定性的方法,其引入主观逻辑(Subjective Logic)来进行建模,并将类别概率建模为一个Dirichlet分布,模型输出的logits作为主观意见(subjective opinions)的证据(evidence)。
Softmax概率的问题
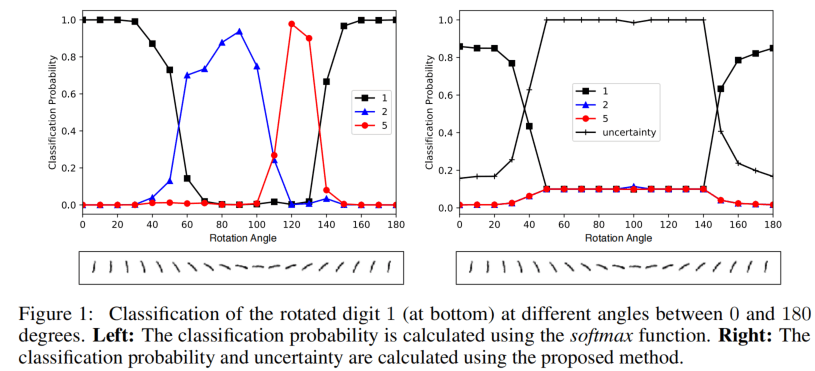
在使用网络对MNIST进行分类时,一般模型最后就输出logits然后通过softmax转换成概率,并使用交叉熵进行优化。
上图左边是对数字1进行旋转得到各个分类的概率,可以看到,在将1逐渐转到90度附近时,类别“1”的概率下降,但是对于横着的“1”,虽然不属于任何数字,但是“2”和“5”类别的概率却非常高,此时模型在“不懂装懂”。
上图右边则是使用EDL建模之后的情况,除了每个类的概率,还有一个不确信度的输出,可以看到,在横着“1”时,其他类别的概率都比较低,而不确定性很高,因为这是一个不确定的预测,模型无法确定它看到的是哪个数字(实际上哪个数字都不对)。
主观逻辑
EDL是基于主观逻辑的,主观逻辑则是Audun Jøsang教授写了一本书来介绍的学科,这里给出其PPT和Opinion Visualization Demo (universitetetioslo.no)。
在标准的逻辑概念里,一个命题要么是真的,要么是假的;在概率逻辑中,观点则可以表示为的概率。然而,现实中人类做判断都不是完全确定的,也不能完全确信某个观点的“正确率”,我们生活的世界是主观的。目前的神经网络模型无法表达“我不知道”这个概念,就像让一个小学生来做微积分题一样,小学生会说“我不知道”,而不是随便写一个数字。因为模型都会输出一个和为1的概率,这种建模就不可能得到“不确定性”。即使是的概率也只是表示正和负的概率都为0.5,而不是“不确定”。
⚠️以下以二元主观逻辑为例进行说明
主观逻辑(Subjective Logic)包含以下几个概念:
-
opinion:直译是“意见”,即一个人对某件事情的主观的看法。是一个函数,包含了belief mass、uncertainty mass、base rate,在二元时是一个四元组,如下所示

-
belief mass是认为某个事情是true的相信程度
-
uncertainty是1减去所有类别的相信程度,剩下的不确信度
-
base rate是先验概率,指在做出判断之前属于各个类别的概率
的取值范围均为,且,即belief信念总和为1,分布在正类、负类和不确定度上。
- 当时,表示绝对的True
- 当时,表示绝对的False
- 当时,表示传统的没有不确信度的概率
- 当时,是比较一般性的带有不确信度的情况;当时,则是完全不确定。
一个二元的意见可以用一个等边三角形表示:
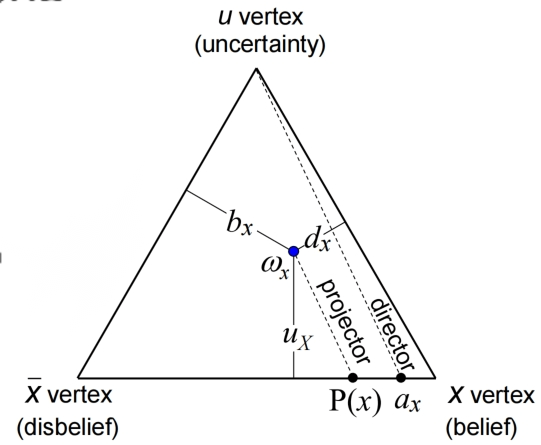
这是一些特殊情况在三角形上的点:
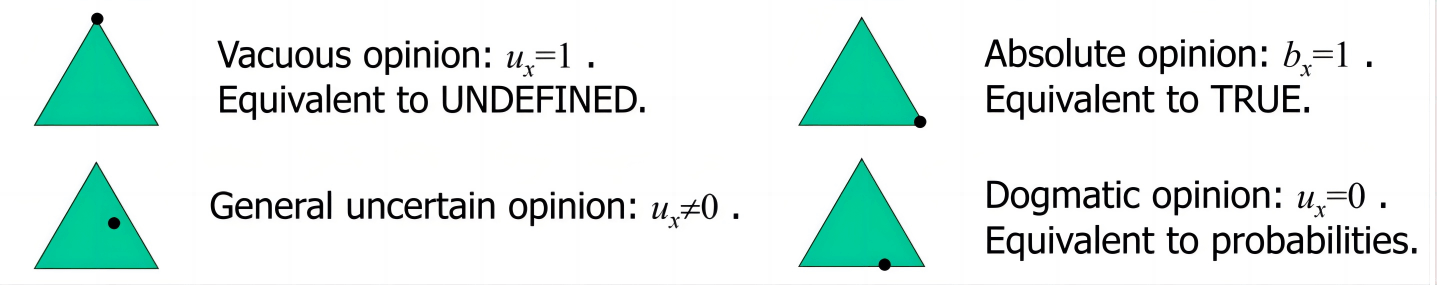
一个二元意见同样也可以用一个Beta分布表示
Beta分布有和两个参数,假设观察到正类有个、负类有个,那 ,其中是不同类别的先验比率,是给先验加权的定值,一般定义为类别数量。和的区别在于,前者对于多分类问题每个类别会有一个对应的,而后者是所有类别共享一个的;前者在二元意见表示中也存在,而仅在Beta分布中存在。
在类别数固定的情况下,一个Beta分布也可以由三个参数表示。
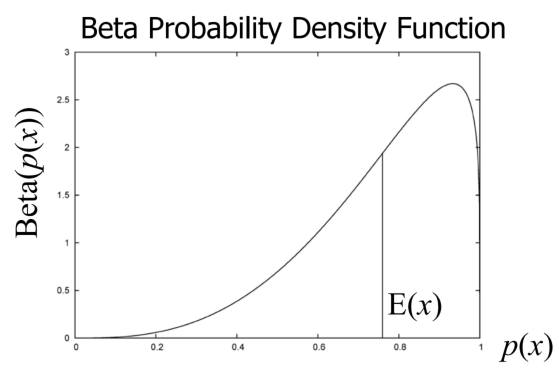
二元意见和Beta分布两者间的互相转换通过下面这两组公式进行:
可以在作者的网页Demo上玩一玩:Opinion Visualization Demo (universitetetioslo.no)
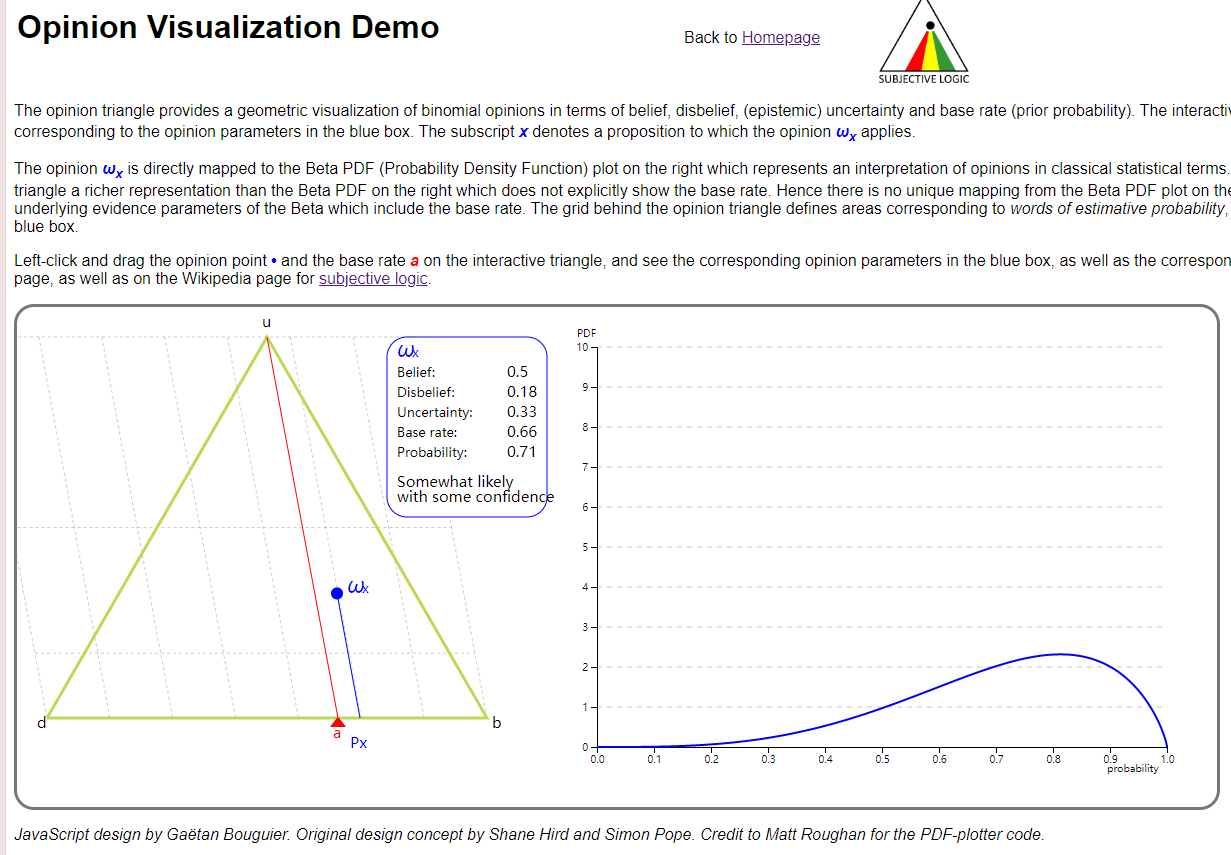
如上图所示,二元意见还可以投影得到一个传统的概率,即
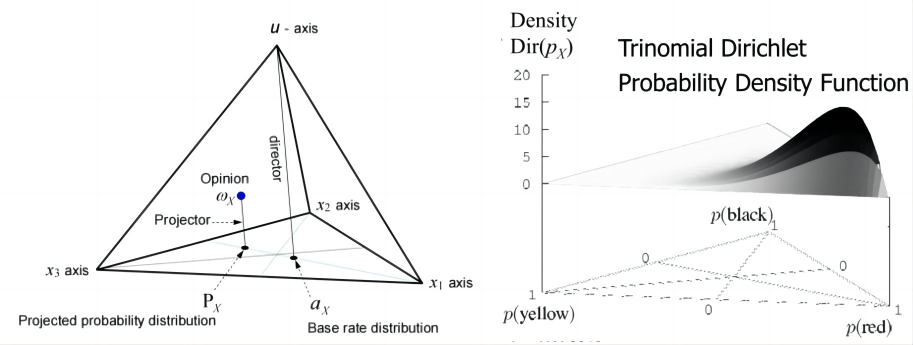
三元主观逻辑则拓展到用圆锥和Dirichlet分布表示:
EDL:从Opinion中学习
有了主观逻辑的理论基础,EDL就能在其之上设计新的损失函数。
**首先定义符号,**假设网络要对个类别进行分类,类别没有先验,每个类别有belief ,还有不确信度,它们加在一起是1:。
belief则由evidence得到:。
evidence的取值范围为正数,且可以对应Dirichlet分布的参数:。
而Dirichlet分布的均值为概率的期望:。
Type II Maximum Likelihood 损失函数
将原来最后一层的softmax将被替换为非负的激活层,比如ReLU,用来让网络输出evidence vector,用表示,则Dirichlet的参数就是。由此构建最大似然的损失函数:
基本就是概率得到的方式不一样,此外和交叉熵很像。
Bayes risk 损失函数
umm,看不懂,但是公式是这样的:
其中是digamma function
Bayes risk 引用在平方根上的损失函数
也看不懂,但是公式是这样的:
正则项
大概是得到的Dirichlet分布要远离“不确定”的均匀分布。
参考文献
Evidential Deep Learning to Quantify Classification Uncertainty 论文阅读笔记 - 知乎 (zhihu.com)
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!